2.3.4.A1 のバックアップ(No.8)
【2】数学 Mathematics
【2.3】解析学 Analysis
【2.3.4】微積分 Calculus
【2.3.4.A】微分 Derivative
【2.3.4.A1】微分の定義
contents
※ このページではMathJax を利用しております。環境によっては数式を表示できないかもしれません。
※証明は別ページで行います。
微分の定義
微分可能
| \( y=f(x) \)が\( x=a \)付近で定義されていること。 |
| \( \displaystyle \lim_{h \to 0 } \frac{f(a+h)-f(a)}{h} \) が有限値に存在すること。 |
上二点を満たすとき、微分可能という。また上式の値を微分係数という。
微分係数の図形的意味
微分係数の\( \displaystyle f'(a) = \lim_{h \to 0 } \frac{f(a+h)-f(a)}{h} \)の図形的意味を考えてみる。
\( h \)を\( x \)の増分、すなわち、\( \Delta x \)と考えると、\( f(a+h)-f(a) \)は\( y \)の増分、すなわち\( \Delta y \)と考えることができる。
そうすると、\( \displaystyle \frac{f(a+h)-f(a)}{h} \) は 点\( (a,f(a)) \)と点\( (a+h,f(a+h)) \)の傾きとなる。
ref
\( h \)を0に近づけると、傾きの線は点\( (a,f(a)) \)にピタッと寄り添う感じになる……
すなわち、点\( (a,f(a)) \)での接線の傾きとなる。
導関数
微分係数\( f'(a) \)を観察してみると、文字\( a \)を\( x \)に置き換えると、新たな関数が出来るように見える。
ここで、導関数の定義は、増分の考え方を用いて以下のようになる。
【\( x \)で微分可能の定義】
前提として、
- 関数 \( y=f(x) \) について、\( x \) は自由変数であり、\( y \) は\( x \)の従属変数
(つまり、\( x \)によって\( y \)の値が決まる。) - \( x \to x+\Delta x \\ y \to y+\Delta y \)
ただし、\( y+\Delta y = f(x + \Delta x) \)
このとき、\( x \to x+\Delta x \)の平均変化率は次のように表せる。
| \( \displaystyle \frac{\Delta y}{\Delta x} = A(x) + \sigma(x,\Delta x) \) |
つまり、\( x \)のみに依存する関数\( A(x) \)と、
\( x,\Delta x \)の両方に依存する\( \sigma(x,\Delta x) \)で表せる。
このとき、『\( f(x) \)で微分可能である』ことと、以下の条件が必要十分条件となる。
| \( \displaystyle \frac{\Delta y}{\Delta x} = A(x) + \sigma(x,\Delta x) \\ \displaystyle \lim_{\Delta x \to 0} \sigma(x,\Delta x) = 0 \) |
また、このとき、\( A(x)=f'(x) \)と書ける。
<ここちょっと工事中です。>
 マスクの資料保管庫
マスクの資料保管庫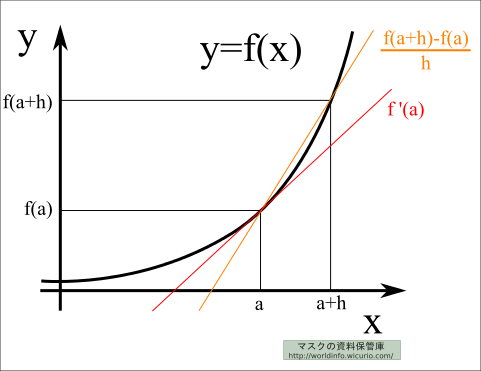
pcomment
コメントはありません。 Comments/2.3.4.A1