数列の極限 のバックアップ(No.4)
【2】数学 Mathematics
【2.3】解析学
【2.3.1】解析学基礎
【2.3.1.d】数列の極限 Limit of a sequence
contents
※1 このページではMathJax を利用しております。環境によっては数式を表示できないかもしれません。
※2 この項で数列という場合、特に言わなくても無限数列のことを指します。
とりあえず単位を取りたい
数列の収束の証明の定型文
\( \displaystyle \lim_{x \to \infty} a_n=a \) の証明:定型文
任意な \( \epsilon>0 \) に対して、
1つの自然数を \( N> ( \epsilon の式 ) \) となるようにとれば、
\( n>N \) ならば、\( | a_n - a | = \fbox{nの式} < \fbox{Nの式} <\epsilon \)
数列の無限大への発散の証明の定型文
\( a_n が \infty に発散する証明:定型文 \)
任意な \( M>0 \) に対して、
1つの自然数を \( N> ( \epsilon の式 ) \) となるようにとれば、
\( n>N ならば、 | a_n - a | = \fbox{nの式} > \fbox{Nの式} >M \)
数列の極限
高校でも習った通り、数列の極限には以下のパターンがある。
- ある値に収束する
- 発散
- 無限大に発散する
- 振動
この3パターンについて、より厳密に考える。
数列の収束
収束の定義(ε-N論法)
高校レベルにおいては、数列の「収束」は、
「\( n \)が限りなく大きくなると、 \( a_n \) がある値 \( \alpha \)無限に近づくとき、 \( \alpha \)に収束するという。」
また、このとき、
\( \displaystyle \lim_{x \to \infty} a_n= \alpha \) または\( a_n \to \alpha ( x \to \infty ) \)と書ける。
しかし、これは厳密に考えると正確な表現とはいえない。
厳密な収束の定義は以下のようになる。
【ε-N論法(数列の収束の定義)】 [#DefinitionOfConvergentOfSequence]
「任意な正の \( \epsilon \)について( \( \forall \epsilon > 0 \) ) 、
それに対して適切に \( N \) をとれば、( \( \exists N \in \mathbb{N} \) ) 、
\( N \)より大きい全ての\( n \) に対して、( \( \forall n > N \) ) 、
\( |a_n - \alpha| < \epsilon \) とすることができる。 」
ε-N論法の意味
上のように収束の定義を言われて、すぐにこれを理解できるかというと、できる人はできるが、おそらく多くの人はちょっと厳しいのではないのだろうか。
というわけで、その意味を詳しく見ていく。
\( a_n \)を直接扱うのはちょっと大変なので、\( |a_n-\alpha| \)について考える。
もし、\( a_n \)が\( \alpha \)に収束すると考えると、下の図のようになる。
ref
\( \epsilon \)の値を適当に(サイコロでも振って)決めてみると、
上の図のようにグラフが波打ってれば、\( |a_n-\alpha| \) が\( \epsilon \)を下回ることは複数回ある。
いっかい下回ったとしても、また\( \epsilon \)より多くなりことも、ありうる。
しかし、もし、\( a_n \)が収束する(つまり、nが大きくなるほど\( |a_n-\alpha| \) が0に近づいていく)なら、ここを最後に、二度と\( |a_n-\alpha| \) が\( \epsilon \)よりも大きくならない、そんなポイントがあるはずだ……と考えてみる。
そのポイントが上図のNであり、Nより先のnについては、必ず\( |a_n-\alpha| \)は\( \epsilon \)より小さくなっている。
また(サイコロでも振りなおして)\( \epsilon \) の値を決めてやる。
そうすると、うまーくNの値を取ってやれば、同じように、Nから先は、\( \epsilon \) より小さいようにすることができる。
\( \epsilon \) をどんなにいじっても、どんなに小さくしても、うまーくNを決めてしまえば、Nから先は、\( \epsilon \) より小さい……これが収束である。
とはいえ、\( \epsilon \) が変わる度にNを定めていては、無限に証明を書く羽目になってしまう。そこで、Nを\( \epsilon \) の式で書いてみてはどうだろうか?(次章へ続く!)
数列の収束の証明の定型文
では、実際に具体的な\( a_n \)を与えられたとき、証明する手続きを考えてみると、「うまーくNを、\( \epsilon \) の式で表したら、\( | a_n - \alpha | \) が\( \epsilon \)より小さくなった。」 というふうになる。これをちゃんと書けば、
【\( \displaystyle \lim_{x \to \infty} a_n=a \) の証明:定型文 】
任意な \( \epsilon>0 \) に対して、
1つの自然数を \( N> ( \epsilon の式 ) \) となるようにとれば、
\( n>N \) ならば、\( | a_n - \alpha | = \fbox{nの式} < \fbox{Nの式} <\epsilon \)
このとき、具体的な\( a_n \)が与えられていれば、
\( | a_n - \alpha | = \fbox{nの式} < \fbox{Nの式} <\epsilon \)
の部分は単純な式変形で決められる。
そして、\( N> ( \epsilon の式 ) \)は、\( \fbox{Nの式} <\epsilon \) を式変形すれば書ける。
実際に使ってみる
【問題:\( \displaystyle a_n= \frac{1}{n} \) の極限を求めよ】
【考え方】
\( \displaystyle | a_n - \alpha | \) \( \displaystyle = |\frac{1}{n}-0| \) \( \displaystyle = \frac{1}{n} \)
…… \( \displaystyle N<n \)より、
\( \displaystyle \frac{1}{n} < \frac{1}{N} <\epsilon \)
よって、式変形すると、
\( \displaystyle N > \frac{1}{\epsilon} \)
これで、\( \epsilon \)の式が求まったので、証明文は以下のように書ける。
【\( \displaystyle \lim_{x \to \infty} \frac{1}{n}=0 \) の証明】
任意な \( \epsilon>0 \) に対して、
1つの自然数を \( \displaystyle N> \frac{1}{\epsilon} \) となるようにとれば、
\( n>N \) ならば、\( \displaystyle | a_n - \alpha | = \frac{1}{n} < \frac{1}{N} <\epsilon \)
 マスクの資料保管庫
マスクの資料保管庫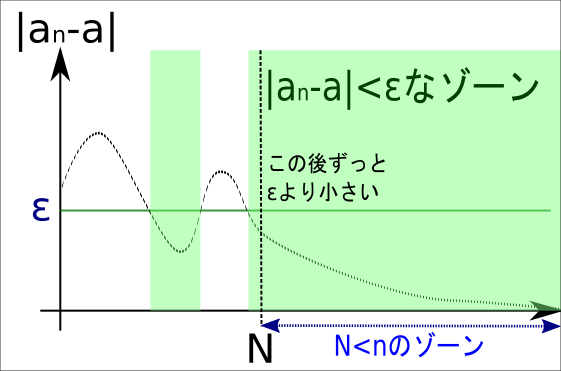

pcomment
最新の10件を表示しています。 コメントページを参照