2.3.4.A1 のバックアップ(No.3)
【2】数学 Mathematics
【2.3】解析学 Analysis
【2.3.2】微積分 Calculus
【2.3.2.a】微分 Derivative
contents
※ このページではMathJax を利用しております。環境によっては数式を表示できないかもしれません。
微分の定義
微分可能
『1』\( y=f(x) \)が\( x=a \)付近で定義されていること。
『2』\( \displaystyle \lim_{h \to 0 } \frac{f(a+h)-f(a)}{h} \) が有限値に存在すること。
上二点を満たすとき、微分可能という。また上式の値を微分係数という。
微分係数の図形的意味
微分係数の\( \displaystyle f'(a) = \lim_{h \to 0 } \frac{f(a+h)-f(a)}{h} \)の図形的意味を考えてみる。
\( h \)を\( x \)の増分、すなわち、\( \Delta x \)と考えると、\( f(a+h)-f(a) \)は\( y \)の増分、すなわち\( \Delta y \)と考えることができる。
そうすると、\( \displaystyle \frac{f(a+h)-f(a)}{h} \) は 点\( (a,f(a)) \)と点\( (a+h,f(a+h)) \)の傾きとなる。
ref
\( h \)を0に近づけると、傾きの線は点\( (a,f(a)) \)にピタッと寄り添う感じになる……
すなわち、点\( (a,f(a)) \)での接線の傾きとなる。
導関数
微分係数\( f'(a) \)を観察してみると、文字\( a \)を\( x \)に置き換えると、新たな関数が出来るように見える。
ここで、導関数の定義は、増分の考え方を用いて以下のようになる。
【\( x \)で微分可能の定義】
以下執筆中
参考
解析学
Nishitani Tatsuo|大阪大学大学院理学研究科数学専攻・理学部数学科
 マスクの資料保管庫
マスクの資料保管庫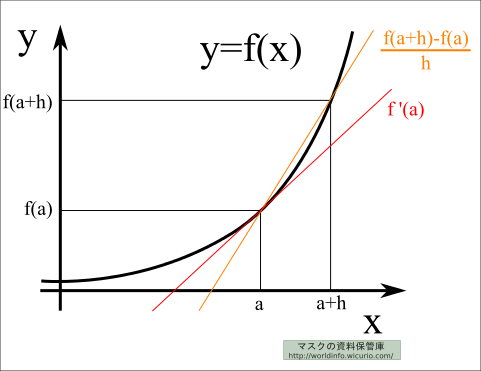
pcomment
コメントはありません。 Comments/2.3.4.A1