数列の極限 のバックアップ(No.2)

• バックアップ一覧
• 差分 を表示
• 現在との差分 を表示
• 現在との差分 - Visual を表示
• ソース を表示
• 数列の極限 へ行く。
  • 1 (2017-08-21 (月) 09:45:57)
  • 2 (2017-08-21 (月) 11:14:40)
  • 3 (2017-08-21 (月) 14:52:52)
  • 4 (2017-08-21 (月) 15:58:55)
  • 5 (2017-08-22 (火) 11:51:17)
  • 6 (2018-10-30 (火) 17:21:01)

【2】数学 Mathematics
【2.3】解析学
【2.3.1】解析学基礎
【2.3.1.d】数列の極限 Limit of a sequence

※1 このページではMathJax を利用しております。環境によっては数式を表示できないかもしれません。

※2 この項で数列という場合、特に言わなくても無限数列のことを指します。

とりあえず単位を取りたい

数列の収束の証明の定型文

\( \displaystyle \lim_{x \to \infty} a_n=a \) の証明：定型文

任意な \( \epsilon>0 \) に対して、

1つの自然数を \( N> ( \epsilon の式 ) \) 　となるようにとれば、

\( n>N \) ならば、\( | a_n - a | = \fbox{nの式} < \fbox{Nの式} <\epsilon \)

数列の無限大への発散の証明の定型文

\( a_n が \infty に発散する証明：定型文 \) [#jb4e30a8]

任意な \( M>0 \) に対して、

1つの自然数を \( N> ( \epsilon の式 ) \) 　となるようにとれば、

\( n>N ならば、 | a_n - a | = \fbox{nの式} > \fbox{Nの式} >M \)

収束

収束の定義（ε-N論法）

高校レベルにおいては、数列の「収束」は、

「\( n \)が限りなく大きくなると、 \( a_n \) がある値 \( \alpha \)無限に近づくとき、 \( \alpha \)に収束するという。」

また、このとき、

\( \displaystyle \lim_{x \to \infty} a_n= \alpha \) または\( a_n \to \alpha ( x \to \infty ) \)と書ける。

しかし、これは厳密に考えると正確な表現とはいえない。
厳密な収束の定義は以下のようになる。

【ε-N論法（数列の収束の定義）】 [#DefinitionOfConvergentOfSequence]
「任意な正の \( \epsilon \)について（ \( \forall \epsilon > 0 \) ） 、
それに対して適切に \( N \) をとれば、（ \( \exists N \in \mathbb{N} \) ） 、
\( N \)より大きい全ての\( n \) に対して、（ \( \forall n > N \) ） 、
\( |a_n - \alpha| < \epsilon \) とすることができる。 」

ε-N論法の意味

上のように収束の定義を言われて、すぐにこれを理解できるかというと、できる人はできるが、おそらく多くの人はちょっと厳しいのではないのだろうか。
というわけで、その意味を詳しく見ていく。

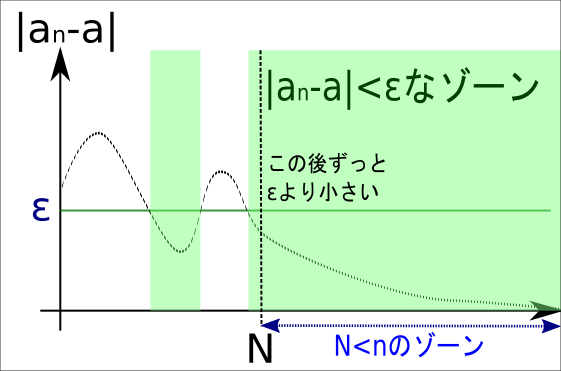
\( a_n \)を直接扱うのはちょっと大変なので、\( |a_n-\alpha| \)について考える。
もし、\( a_n \)が\( \alpha \)に収束すると考えると、下の図のようになる。

ref

ここから先編集中

参考

1年生の数学演習
牛腸 徹 & 清野 和彦