行列式の定義 のバックアップの現在との差分(No.2)
【2.2.3】線形代数学 Linear algebra
【2.2.3.3】行列式 Determinant
【2.2.3.3.1】行列式の定義
| 【2】数学 Mathematics 【2.2】代数学 Algebra 【2.2.3】線形代数学 Linear algebra |
| 【Category.2.2.3.3】 行列式 Determinant |
| 前回 | 【2.2.3.3.1】行列式と面積 |
| 今回 | 【2.2.3.3.2】行列式の定義 |
| 次回 | 【2.2.3.3.3】行列式の計算 |
※ このページではMathJax を利用しております。環境によっては数式を表示できないかもしれません。
contents
前回、二次正方行列の行列式と面積についての関係を見た。
今回は、行列式のちゃんとした定義を追う。
行列式のグラフ上の面積
ちゃんとしたn次行列式の定義
二次の行列式と面積。
すべての成分が\( \mathbb{R} \)(実数)である\( n \)次正方行列\( A \)について、それに対応するスカラー値である行列式は\( \det(A) \)または\( |A| \)と表記する。
二次正方行列を見てみると、二本の縦ベクトルと見ることもできる。
\( A=\left(\begin{array}{ccc}a_x b_x \\a_y b_y \\\end{array}\right) \to \left(\begin{array}{c}a_x\\a_y\\\end{array}\right) と \left(\begin{array}{c}b_x\\b_y\\\end{array}\right) \)
\( \det(A) \)つまり\( |A| \)は、以下の【A-1】、【A-2】、【A-3】の三つの性質により定義される。
【A-1】定義1:列に関する線形多重性
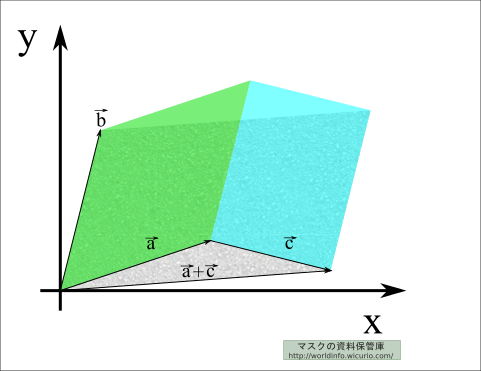
\( a_{pj} = \lambda b_{pj} + \mu c_{pj} , (p=1,2,\dots,n) \) とするとき、
\( \det(A)= \left| \begin{array}{ccccc} a_{11} & \dots & \textcolor{red}{a_{1j}} & \dots & a_{1n} \\ a_{21} & & \textcolor{red}{a_{2j}} & & a_{2n} \\ \vdots & & \vdots & & \vdots \\a_{n1} & \dots & \textcolor{red}{a_{nj}} & \dots & a_{nn} \end{array}\right| \)
(二次正方行列の)行列式とは、この二本の縦ベクトルで作れる平行四辺形の(符号付きの)面積のことを言い、
\( \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| \) あるいは \( \det A \) と表記する。
\( =\left| \begin{array}{ccccc} a_{11} & \dots & \textcolor{red}{\lambda b_{1j} + \mu c{1j}} & \dots & a_{1n} \\ a_{21} & & \textcolor{red}{\lambda b_{2j} + \mu c{2j}} & & a_{2n} \\ \vdots & & \vdots & & \vdots \\a_{n1} & \dots & \textcolor{red}{\lambda b_{nj} + \mu c{nj}} & \dots & a_{nn} \end{array}\right| \)
ref

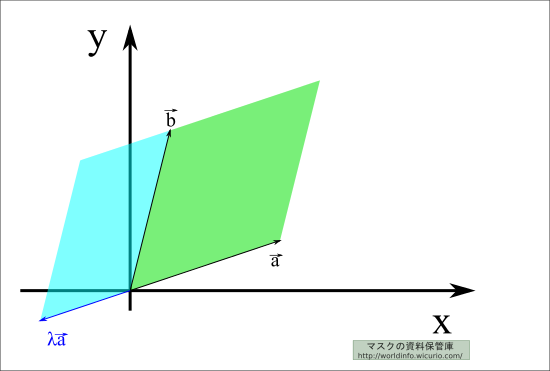
では、片方のベクトルを長くすると、どうなるか。
ref

\( = \textcolor{red}{\lambda} \left| \begin{array}{ccccc} a_{11} & \dots & \textcolor{red}{b_{1j}} & \dots & a_{1n} \\ a_{21} & & \textcolor{red}{b_{2j}} & & a_{2n} \\ \vdots & & \vdots & & \vdots \\a_{n1} & \dots & \textcolor{red}{b_{nj}} & \dots & a_{nn} \end{array}\right| \) \( + \textcolor{red}{\mu} \left| \begin{array}{ccccc} a_{11} & \dots & \textcolor{red}{c_{1j}} & \dots & a_{1n} \\ a_{21} & & \textcolor{red}{c_{2j}} & & a_{2n} \\ \vdots & & \vdots & & \vdots \\a_{n1} & \dots & \textcolor{red}{c_{nj}} & \dots & a_{nn} \end{array}\right| \)
\( \vec{a} \) を \( \lambda \vec{a} \) に伸ばすと、面積も \( \lambda \) 倍になった。
同じことは\( \vec{b} \)を伸ばした場合にも言える。
このことから、
\( \left|\begin{array}{rr} \lambda\ a_x & b_x \\\lambda\ a_y & b_y \\\end{array}\right|= \lambda \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| \)
【A-2】定義2:退化条件
という計算式が成り立つことが分かった。
\( j \) 列と \( k \) 列が等しいとき、\( \det(A)=0 \)
負の面積?
つまり、
では、\( \lambda \) を負にするとどうなるか。
\( a_{pj} = a_{pk} = b_p , (p=1,2,\dots,n) \)のとき、
ref
\( \det(A) \)
負の面積っていうのも、ピンと来ないかもしれないが、反対側に\( \lambda \) 倍になってるのを見ると、負の面積というのも許していいかな……?という風に思える(思って)。
\( = \left| \begin{array}{ccccccc} a_{11} & \dots & \textcolor{red}{a_{1j}} & \dots & \textcolor{red}{a_{1k}} & \dots & a_{1n} \\ a_{21} & & \textcolor{red}{a_{2j}} & & \textcolor{red}{a_{2k}} & & a_{2n} \\ \vdots & & \vdots & & \vdots & & \vdots \\a_{n1} & \dots & \textcolor{red}{a_{nj}} & \dots & \textcolor{red}{a_{nk}} & \dots & a_{nn} \end{array}\right| \)
二次の線形多重性
\( = \left| \begin{array}{ccccccc} a_{11} & \dots & \textcolor{red}{b_{1}} & \dots & \textcolor{red}{b_{1}} & \dots & a_{1n} \\ a_{21} & & \textcolor{red}{b_{2}} & & \textcolor{red}{b_{2}} & & a_{2n} \\ \vdots & & \vdots & & \vdots & & \vdots \\a_{n1} & \dots & \textcolor{red}{b_{n}} & \dots & \textcolor{red}{b_{n}} & \dots & a_{nn} \end{array}\right| \)
\( \large =0 \)
【A-3】定義3:正規化条件
\( \det(E_n)=1 \)
ref
以下執筆中
つまり、単位行列の行列式は \( 1 \)
 マスクの資料保管庫
マスクの資料保管庫
pcomment
コメントはありません。 Comments/行列式の定義