Mandelbrot set のバックアップ(No.5)

• バックアップ一覧
• 差分 を表示
• 現在との差分 を表示
• 現在との差分 - Visual を表示
• ソース を表示
• Mandelbrot set へ行く。
  • 1 (2018-06-12 (火) 00:07:49)
  • 2 (2018-06-12 (火) 01:28:08)
  • 3 (2018-12-17 (月) 21:51:17)
  • 4 (2018-12-17 (月) 23:20:45)
  • 5 (2021-01-23 (土) 02:05:53)

マンデルブロ集合のルール

マンデルブロ集合を一度でも見たことがある人なら、その絵が印象づいて離れないのではないか。少なくとも私はその一人で、大学に入ってグラフ簡単にプロットできる無料のソフトウェアに出会ってから、自分で実際にプロットしたくてたまらなかった思い出がある。

このマンデルブロ集合、下の単純なルールからできている。

\( 複素数z_{k}について、 \large \displaystyle \begin{cases}z_{n+1} = z_{n} + c \\z_{0}^2 = 0 \end{cases}とするとき、\\n \to \infty とすると（つまり無限回計算すると）、\\c の値によって発散する場合としない場合がある。\\発散しないときの c の集合がマンデルブロ集合となる。 \)

このルールに基づいて複素数平面にプロットする下の図形が出現する。

ref

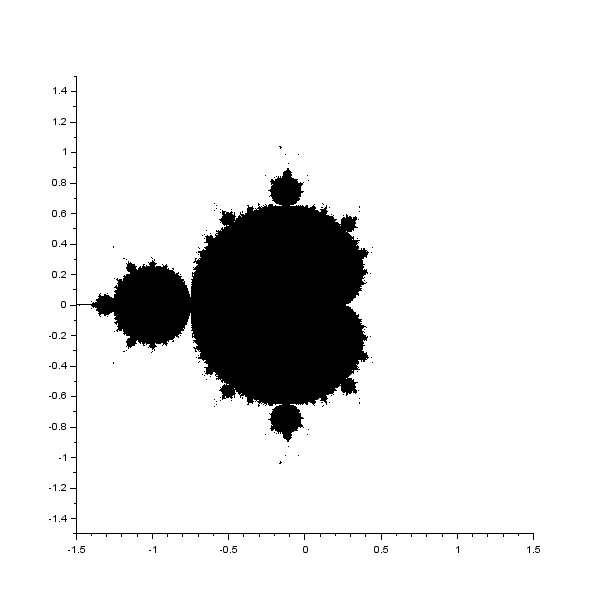
実際的な話

とはいえ、上の話だけだと抽象的すぎて、グラフにプロットするのは大変だと思う。そこで、もうちょっと具体的に考えていきたい。

単純に\( z_{n+1} = z_{n}^2 + c \)を繰り返して発散するかしないかを判定するのは難しい。
ここで、\( |z_n|>2 \)となったら発散する……と考えると解決する。（これがうまくいく理由はそのうち書くかも）

マンデルブロ集合の図集