行列式と面積 のバックアップ(No.2)

• バックアップ一覧
• 差分 を表示
• 現在との差分 を表示
• 現在との差分 - Visual を表示
• ソース を表示
• 行列式と面積 へ行く。
  • 1 (2017-08-22 (火) 23:33:33)
  • 2 (2017-08-25 (金) 13:24:38)
  • 3 (2017-08-29 (火) 13:36:05)
  • 4 (2017-09-08 (金) 21:45:26)

【2.2.3】線形代数学 Linear algebra
【2.2.3.3】行列式 Determinant
【2.2.3.3.1】行列式と面積

※1 このページではMathJax を利用しております。環境によっては数式を表示できないかもしれません。

※2 二次正方行列の行列式の公式と合ってるかの計算は次回でやります。

行列式のグラフ上の面積

二次の行列式と面積。

二次正方行列を見てみると、二本の縦ベクトルと見ることもできる。

\( A=\left(\begin{array}{ccc}a_x 　 b_x \\a_y 　 b_y \\\end{array}\right) \to \left(\begin{array}{c}a_x\\a_y\\\end{array}\right) と \left(\begin{array}{c}b_x\\b_y\\\end{array}\right) \)

（二次正方行列の）行列式とは、この二本の縦ベクトルで作れる平行四辺形の（符号付きの）面積のことを言い、

\( \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| \) あるいは \( \det A \)　と表記する。

ref

では、片方のベクトルを長くすると、どうなるか。

ref

\( \vec{a} \) を \( \lambda \vec{a} \) に伸ばすと、面積も \( \lambda \) 倍になった。

同じことは\( \vec{b} \)を伸ばした場合にも言える。

このことから、

\( \left|\begin{array}{rr} \lambda\ a_x & b_x \\\lambda\ a_y & b_y \\\end{array}\right|= \lambda \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| \)

という計算式が成り立つことが分かった。

負の面積？

では、\( \lambda \) を負にするとどうなるか。

ref

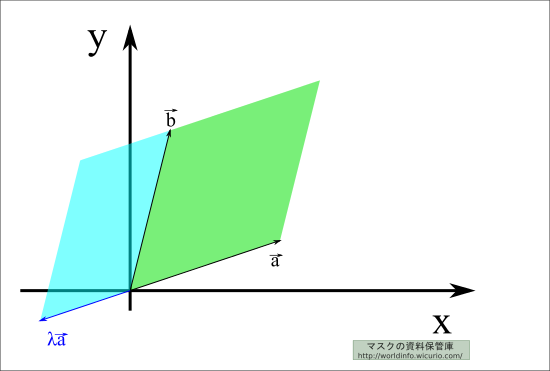
負の面積っていうのも、ピンと来ないかもしれないが、反対側に\( \lambda \) 倍になってるのを見ると、負の面積というのも許していいかな……？という風に思える（思って）。

ベクトルの足し算と面積

では、今度は\( \left|\begin{array}{rr} \ a_x+c_x & b_x \\ a_y+c_y & b_y \\\end{array}\right| \) となっているときを考える。

ref

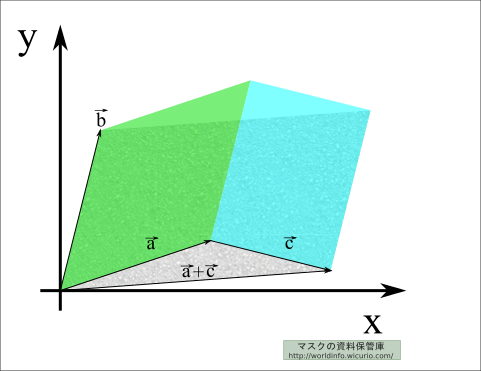
このとき上の図から、\( \vec{a} \)と\( \vec{b} \)の平行四辺形と\( \vec{c} \)と\( \vec{b} \)の平行四辺形とを足し合わせると、\( \vec{a}+\vec{c} \)と\( \vec{b} \)の平行四辺形と同じ面積となってる。
つまり、

\( \left|\begin{array}{rr} a_x+c_x & b_x \\ a_y+c_y & b_y \\\end{array}\right| = \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| + \left|\begin{array}{cc}c_x & b_x \\c_y & b_y \\\end{array}\right| \)

これも、\( \vec{b} \)についておなじことをしても成り立っている。

（二次正方行列の）線形多重性

\( \left|\begin{array}{rr} \lambda\ a_x & b_x \\\lambda\ a_y & b_y \\\end{array}\right|= \lambda \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| \)

と

\( \left|\begin{array}{rr} a_x+c_x & b_x \\ a_y+c_y & b_y \\\end{array}\right| = \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\\end{array}\right| + \left|\begin{array}{cc}c_x & b_x \\c_y & b_y \\\end{array}\right| \)

の二つの式が成り立ってると考えると、以下の式にまとめられる。

\( \left|\begin{array}{rr} \lambda a_x + \mu c_x & b_x \\ \lambda a_y + \mu c_y & b_y \\ \end{array}\right| = \lambda \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \\ \end{array}\right| + \mu \left|\begin{array}{cc}c_x & b_x \\c_y & b_y \\ \end{array}\right| \)

また、\( \vec{b} \)のほうについても同様に、

\( \left|\begin{array}{rr} a_x & \lambda b_x + \mu c_x \\ a_y & \lambda b_y + \mu c_y \end{array}\right| = \lambda \left|\begin{array}{cc}a_x & b_x \\a_y & b_y \end{array}\right| + \mu \left|\begin{array}{cc}a_x & c_x \\a_y & c_y \end{array}\right| \)

コメント